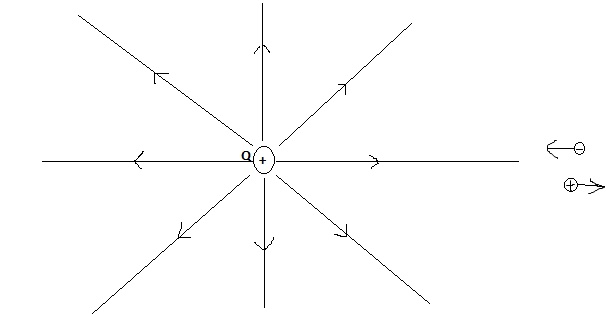
Electric Field due to charge particle
When exploring the fundamental concepts of electromagnetism, the generation of electric field due to charge particle plays a crucial role. Whether you’re a student delving into physics or a professional reviewing core principles, understanding how a charged particle influences its surrounding space through its electric field is essential. In this post, we’ll delve into the concept of the electric field created by a charged particle and explore its significance in various applications.
What is the Electric Field (E)?
The electric field (E) is a vector field that represents the force exerted by a charged particle on other charges within its vicinity. It’s a fundamental concept introduced by Michael Faraday and is a cornerstone of electromagnetism. The electric field due to charge particle in space is defined as the force per unit charge experienced by a positive test charge placed at that point.
How is the Electric Field Calculated?
For a point charge q, the electric field E at a distance r from the charge is given by Coulomb’s law:
[math]F = \frac{k \cdot |q_1 \cdot q_2|}{r^2}[/math]
where:
- k is Coulomb’s constant and its value is [math]8.99 \times 10^9 \, \text{N m}^2/\text{C}^2[/math]
- [math]\text{q}[/math] is the magnitude of the charge of the particle,
- r is the distance from the charge to the point where the field is being calculated, and
- [math]\hat{r}[/math] is a unit vector pointing from the charge to the location where the electric field is being measured.
This formula indicates that the electric field decreases with the square of the distance from the charge. The direction of the electric field vector is radially outward from a positive charge and radially inward towards a negative charge.
Key Characteristics of the Electric Field
Direction:
The electric field created by a positive charge radiates outward, while it converges inward for a negative charge. This direction is essential for understanding how forces are exerted on other charges within the field.
Field Lines
Electric field lines are used to visualize the field. They start from positive charges and end at negative charges. The density of these lines represents the strength of the field; denser lines indicate stronger fields.
Superposition Principle
When dealing with multiple charges, the total electric field at any point is the vector sum of the electric fields due to each charge. This principle allows for the analysis of complex charge distributions.
Practical Applications
Understanding the electric field due to a charged particle has several practical applications:
Electrostatics
The concept is fundamental in electrostatics, which deals with stationary electric charges. It helps in designing capacitors and understanding charge distributions on conductors and insulators.
Particle Physics
In particle accelerators, the electric field due to charge particle are crucial for steering and focusing particle beams.
Electronics
The behavior of electrons in semiconductor devices and integrated circuits is influenced by electric fields. This understanding aids in designing more efficient electronic components.
Medical Applications
Electric fields are used in various medical technologies, such as electrophysiological measurements and certain types of imaging techniques.
Summary
The electric field due to charged particle is a fundamental concept in electromagnetism that has far-reaching implications across various fields of science and engineering. By understanding how this field is calculated, its characteristics, and its practical applications, you gain insights into the interactions of charged particles and their effects on their surroundings.
Whether you’re a physics enthusiast, an engineering student, or a professional in the field, grasping the principles behind the electric field due to a charged particle is crucial for a deeper understanding of electromagnetic phenomena. If you have any questions or comments about the electric field or related topics, feel free to leave them in the comment box below!
written by Hilal Khan.